pKS- und pKB-Wert
Säure-Base-Reaktionen sind, wie alle chemischen Reaktionen, Gleichgewichtsreaktionen, die sich durch das Massenwirkungsgesetz beschreiben lassen. Aus dem Massenwirkungsgesetz lassen sich stoffspezifische Konstanten ableiten, die die "Stärke" einer Säure oder Base in Form des pKS- bzw. pKB-Wertes angeben.
Brønstedt-Definition als Gleichgewichtsreaktion
In der Definition von Brønstedt sind Säuren Protonendonatoren und Basen Protonenakzeptoren. Eine Säure-Base-Reaktion ist damit immer eine Protonenübertragung (vgl.: Säure-Base-Definitionen). Betrachten wir im Folgenden ein paar Beispiele:
- Salzsäure: HCl + H2O ⇄ H3O+ + Cl- Säure Base Säure Base
- Schwefelsäure: H2SO4 + 2 H2O ⇄ 2 H3O+ + SO42- Säure Base Säure Base
- Phosphorsäure: H3PO4 + 3 H2O ⇄ 3 H3O+ + PO43- Säure Base Säure Base
- Ammoniak: NH3 + H2O ⇄ NH4+ + OH- Base Säure Säure Base
Bei den obigen Beispielen gibt es sowohl für die Hin- als auch für die Rückreaktion je eine Säure und eine Base. Die korrespondierenden Säure-Base-Paare sind jeweils durch die identischen Farben der Worte Säure bzw. Base unter den Formeln zu erkennen. Auf jedes dieser Gleichgewichte ließe sich theoretisch das Massenwirkungsgesetz anwenden:
Anwendung des Massenwirkungsgesetzes

Die in der Abbildung dargestellte allgemeine Form des Massenwirkungsgesetzes soll im Folgenden zunächst auf "einprotonige" Säuren (z.B. HCl) und Basen (z.B. NH3) angewendet werden, ehe dann die Übertragung auf mehrprotonige Säuren und Basen erfolgt.
Einprotonige Säuren
Betrachten wir zunächst beispielhaft die Salzsäure. Salzsäure ist in Wasser gelöster Chlorwasserstoff (HCl). Beim Lösen in Wasser dissoziiert der Protonendonator Chlorwasserstoff indem er ein Proton an das Wasser abgibt. Hierbei reagiert Chlorwasserstoff als Säure und das Wasser als Protonenakzeptor, also als Base. Die Reaktion ist eine Gleichgewichtsreaktion, wobei in der Rückreaktion das Hydroniumion (H3O+) als Säure und das Chloridion als Base reagieren.
- Salzsäure: HCl + H2O ⇄ H3O+ + Cl- Säure Base Säure Base
Auf diese Reaktion lässt sich das Massenwirkungsgesetz wie auf jede andere Gleichgewichtsreaktion anwenden:
HCl + H2O ⇄ H3O+ + Cl-

Da die Gleichgewichtskonstante Kc eine Konstante für die betrachtete Reaktion ist, stellt sich in dem Bruch des Massenwirkungsgesetzes immer das gleiche Verhältnis aus Produkt- und Eduktkonzentrationen ein, denn nur dann ergibt der betrachtete Quotient immer denselben Wert. Theoretisch könnte man jetzt für alle Säuren den Wert für Kc in der Protolysereaktion messen und in Tabellenwerken auflisten und so die Neigung einer Säure zur Protonenabgabe in Zahlen beschreiben....
Der pKS-Wert
Tatsächlich gibt es einen einfacheren Weg die Neigung von Säuren zur Protonenabgabe in einer Zahl auszudrücken. Da ALLE Säuren eine strukturell identische Protolysereaktion zeigen, betrachten wir im Folgenden die allgemeine Reaktion der Säure HA, die mit Wasser zu einem Hydroniumion und einem Säurerestion A- reagiert. Das A steht dabei als Platzhalter für einen beliebigen Säurerest.

Nimmt man an, dass die Lösung nicht all zu konzentriert ist, kann die Konzentration des Wassers als nahezu konstant angesehen werden. Der Grund hierfür ist, dass in solchen verdünnten Lösungen fast nur Wasser im Gefäß ist und der gelöste Stoff nur einen vernachlässigbar kleinen Effekt auf das Volumen hat. In diesem Fall ändert sich die Konzentration des Wassers durch die Zugabe der Säure HA nahezu nicht.
Multipliziert man dann den Term für Kc auf beiden Seiten mit der Konzentration des Wassers, fällt diese auf der rechten Seite der Gleichung weg. Auf der linken Seite der Gleichung steht dann das Produkt c(H2O)·Kc. Unter der Annahme, dass die Wasserkonzentration näherungsweise eine konstante Größe ist, ist auch ihr Produkt mit der Gleichgewichtskonstanten Kc wieder eine Konstante, die Säurekonstante KS.
Aus dieser Säurekonstante lässt sich der pKS-Wert als negativer dekadischer Logarithmus definieren. Dieser pKS-Wert wurde für nahezu alle Säuren bestimmt und wird üblicherweise angegeben um die "Stärke" einer Säure, also ihre Neigung ein Proton abzugeben, zu beschreiben.
Je stärker eine Säure ist, desto stärker ist ihre Neigung als Protonendonator zu reagieren und desto größer ist der KS-Wert und desto kleiner ist der pKS-Wert.
Einprotonige Basen
Betrachten wir auch bei den Basen zunächst wieder ein Beispiel, den Ammoniak (NH3). Ammoniak reagiert mit Wasser als Base, also als Protonenakzeptor. Das Wasser ist in dieser Reaktion die Säure, also der Protonendonator. In der Reaktion entstehen Ammoniumionen (NH4+) und Hydroxidionen (OH-).
- Ammoniak: NH3 + H2O ⇄ NH4+ + OH- Base Säure Säure Base
In der Rückreaktion reagiert entsprechend das Ammoniumion als Säure und das Hydroxidion als Base. Das Hydroxidion ist auch dafür verantwortlich, dass wässrige Lösungen des Ammoniaks basisch sind, d.h. einen pH-Wert über 7 zeigen.
Auch die Reaktion des Ammoniaks mit Wasser ist eine Gleichgewichtsreaktion, für die das Massenwirkungsgesetz gilt:
NH3 + H2O ⇄ NH4+ + OH-

Wie weiter oben bei den Säuren schon erwähnt, ist Kc eine Konstante, die für diese Reaktion immer den gleichen Wert hat. In der Folge stellt sich für den Bruch rechts vom Gelichzeichen immer das gleiche Konzentrationsverhältnis ein also das gleiche Verhältnis von Produkt- zu Eduktkonzentrationen ein.
Der pKB-Wert
Analog zum KS- und pKS-Wert bei den Säuren lässt sich für die Reaktion der Basen ein KB- und pKB-Wert definieren. Betrachten wir dazu die Reaktion einer beliebigen Base B- mit Wasser zur korrespondierenden Säure HB und einem Hydroxidion:

Wie schon bei der Herleitung von KS- und pKS-Wert lässt sich auch hier wieder die Konzentration des Wassers als näherungsweise konstant und unabhängig von den anderen Konzentrationen ansehen, solange man nur verdünnte Lösungen betrachtet. Durch Multiplikation des Terms für Kc erhält man dann auf der linken Seite des Gleichheitszeichens das in diesem Fall ebenfalls konstante Produkt c(H2O)·Kc, dass wir als Basenkonstante KB definieren können.
Aus der Basenkonstante KB lässt sich dann der pKB-Wert als negativer dekadischer Logarithmus definieren. Dieser pKB-Wert wurde für nahezu alle Basen bestimmt und lässt sich wie schon der pKS-Wert in Tabellen nachschlagen. Der pKB-Wert beschreibt die "Stärke" einer Base, d.h. ihre Neigung bei Reaktionen mit einem Protonendonator ein Proton aufzunehmen.
Je stärker eine Base ist, desto höher ist ihre Neigung als Protonenakzeptor zu reagieren und desto größer ist der KB-Wert und desto kleiner ist der pKB-Wert.
Der Zusammenhang zwischen pKB-Wert und pKS-Wert
Betrachten wir ein korrespondierendes Säure-Base-Paar, wie HCl und Cl- oder NH4+ und NH3 oder allgemein HB und B-, so scheint ein mathematischer Zusammenhang zwischen dem pKS-Wert der Säure und dem pKB-Wert der Base naheliegend. In der folgenden Tabelle wird die Reaktion von HB als Säure in der linken Spalte mit der von B- als konjugierter Base in der rechten Spalte verglichen:
| HB als Säure | B- als Base |
|---|---|
| HB + H2O ⇄ B- + H3O+ | B- + H2O ⇄ HB + OH- |
 |
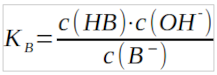 |
Betrachtet man die Terme für KS und KB, fällt auf, dass sie beide einen Quotienten aus den Konzentrationen der Säure und der Base enthalten, nur das der eine Quotient dem Kehrwert des anderen entspricht. Wenn man nun KS und KB miteinander multipliziert, fallen die Konzentrationen von Säure und Base einfach weg:

Von dem resultierenden Produkt bildet man nun den negativen dekadischen Logarithmus, um anstelle von KS und KB pKS und pKB zu erhalten:

pKS + pKB = 14
Mehrprotonige Säuren und Basen
Mehrprotonige Säuren und Basen benötigen eigentlich keine eigenständige Betrachtung, denn die Reaktion der einzelnen Protolysestufen erfolgt nacheinander und jede stellt eine eigene Gleichgewichtsreaktion dar, die mit je einer eigenen Säure- und Basekonstanten beschrieben wird. Betrachten wir als Beispiel die dreiprotonige Säure Phosphorsäure wie oben schon dargestellt:
- Phosphorsäure: H3PO4 + 3 H2O ⇄ 3 H3O+ + PO43- Säure Base Säure Base
Tatsächlich reagiert das Molekül der Phosphorsäure nicht in einer einzigen Reaktion mit drei Wassermolekülen gleichzeitig unter Abspaltung aller drei Protonen. Stattdessen ist jede einzelne Protonenabspaltung ein eigenes Gleichgewicht:
| Gleichgewicht | pKS | pKB | |
|---|---|---|---|
| 1. Stufe | H3PO4 + H2O ⇄ H2PO4- + H3O+ | 2,16 | 11,84 |
| 2. Stufe | H2PO4- + H2O ⇄ HPO42- + H3O+ | 7,21 | 6,79 |
| 3. Stufe | HPO42- + H2O ⇄ PO43- + H3O+ | 12,32 | 1,68 |
Von den drei Säuren der obigen Tabelle, Phosphorsäure (H3PO4), Dihydrogenphosphat (H2PO4-) und Hydrogenphosphat ((HPO42-), ist die Phosphorsäure die Stärkste, denn ihr pKS-Wert ist der Kleinste. Gleichzeitig ist Phosphat (PO43-) die stärkste Base in der Tabelle, denn ihr pKB-Wert ist der Kleinste.
Anwendungen und Rechenbeispiele
Tabellen mit pKS- und pKB-Werten finden sich in jeder Formelsammlung und auf zahlreichen Internetseiten, z.B. bei Wikibooks oder bei Wikipedia. Für die folgenden Berechnungen werden die Werte von der Wikipedia-Seite benutzt.
pH-Wert von Essig
Handelsüblicher Essig hat eine Säurekonzentration von üblicherweise etwas unter 1 mol/L. Der Einfachheit halber nehme ich im Folgenden einfach an, es sei genau 1 mol/L. Nimmt man an, dass von den insgesamt 1 mol/L ein Teil, nämlich x mol/L, ein Proton abgespalten hat, ergibt sich folgendes:
H3CCOOH + H2O ⇄ H3CCOO- + H3O+ ohne Glgw: 1 mol/L 0 mol/L 0 mol/L im Glgw: (1-x) mol/L x mol/L x mol/L
Der pKS-Wert von Essigsäure ist 4,75, womit der KS-Wert 10-4,75 mol/L ist. Setzt man nun die vorstehenden Werte für die Konzentrationen im Gleichgewicht in den Term für KS ein und stellt nach x um, so erhält man das Folgende Ergebnis:

In der dargestellten Rechnung sieht man in der ersten Zeile zunächst den Term für KS für die obige Reaktion und darunter dann die eingesetzten Konzentrationen mit x mol/L für die Acetationen (H3CCOO-) und die gleich große Hydroniumkonzentration (H3O+). Die Konzentration der im Gleichgewicht noch vorhandenen Essigsäure ist entsprechend um x mol/L verringert. Division durch die Einheit und Kürzen der verbleibenden Einheit liefert eine "einfache" quadratische Gleichung ohne Einheiten, die sich mit Mitteln der Mathematik entsprechend einfach lösen lässt.
Da quadratische Gleichungen mathematisch immer zwei Lösungen haben, erhält man auch hier für x zwei mathematisch mögliche Ergebnisse, 0,0042 und -0,0042. Da x den Zahlenwert der Hydroniumkonzentration angibt, muss das chemisch richtige Ergebnis zwischen 0 und 1 liegen, denn Konzentrationen unter 0 sind nicht möglich und Konzentrationen über 1 mol/L können bei einer Ausgangsmenge von 1 mol/L Essigsäure ebenfalls nicht auftreten. Somit erhalten wir eine Konzentration der Hydroniumionen von 0,0042 mol/L.
Aus dieser Konzentration lässt sich der pH-Wert als negativer dekadischer Logarithmus berechnen, wodurch man den pH-Wert von ca. 2,38 erhält.
pH-Wert von 1 molarem Ammoniak
Im Vergleich zur schwachen Säure Essigsäure im vorherigen Abschnitt wird jetzt der pH-Wert der schwachen Base Ammoniak ebenfalls mit einer Konzentration von 1 mol/L berechnet.
NH3 + H2O ⇄ NH4+ + OH- ohne Glgw: 1 mol/L 0 mol/L 0 mol/L im Glgw: (1-x) mol/L x mol/L x mol/L
Der pKB-Wert von Ammoniak beträgt 4,75 und der KB-Wert somit 10-4,75 mol/L. Setzt man nun die vorstehenden Werte der Konzentrationen im Gleichgewicht in den Term für KB ein und stellt nach x um, so erhält man das folgende Ergebnis:

In der dargestellten Rechnung sieht man in der ersten Zeile zunächst den Term für KB für die obige Reaktion und darunter dann die eingesetzten Konzentrationen mit x mol/L für die Ammoniumionen- (NH4+) und die gleich große Hydroxidionenkonzentration (OH-). Die Konzentration des im Gleichgewicht noch vorhandenen Ammoniaks ist entsprechend um x mol/L verringert. Division durch die Einheit und Kürzen der verbleibenden Einheit liefert ebenso wie im vorherigen Abschnitt eine "einfache" quadratische Gleichung ohne Einheiten, die sich mit Mitteln der Mathematik entsprechend einfach lösen lässt.
Da quadratische Gleichungen mathematisch immer zwei Lösungen haben, erhält man auch hier für x zwei mathematisch mögliche Ergebnisse, 0,0042 und -0,0042. Da x den Zahlenwert der Hydroxidionenkonzentration angibt, muss das chemisch richtige Ergebnis zwischen 0 und 1 liegen, denn Konzentrationen unter 0 sind nicht möglich und Konzentrationen über 1 mol/L können bei einer Ausgangsmenge von 1 mol/L Ammoniak ebenfalls nicht auftreten. Somit erhalten wir eine Konzentration der Hydroxidionen von 0,0042 mol/L.
Aus dieser Konzentration lässt sich der pOH-Wert als negativer dekadischer Logarithmus berechnen, wodurch man den pOH-Wert von ca. 2,38 erhält. Hieraus ergibt sich der pH-Wert durch pH=14-pOH als 11,62, denn in allen ausreichend verdünnten wässrigen Lösungen gilt immer: pH+pOH=14.
Mehrprotonige Säuren und Basen
Da bei mehrprotonigen Säuren und Basen immer mehrere Gleichgewichte vorliegen (s.o.), lassen sich die pH-Wert-Berechnungen für jedes der einzelnen Gleichgewichte genauso durchführen, wie gerade für die einprotonigen Säuren und Basen beschrieben. Leider trifft man dabei auf zwei Probleme:
- Mehrere Gleichgewichte mit mehreren Rechnungen haben auch mehrere Ergebnisse. Welches davon ist richtig?
- Jede der Gleichgewichtsreaktionen beeinflusst die Konzentration der Hydronium- bzw. der Hydroxidionen. Welchen Wert setzt man dann in seiner Rechnung bei den jeweils anderen Gleichgewichten ein?
Die Lösung dieser beiden Probleme ist eine Näherungsrechnung. Es werden einfach nicht alle Gleichgewichte betrachtet, sondern nur dasjenige, dass den pH-Wert maßgeblich beeinflusst. Betrachten wir dazu noch mal die Phosphorsäure, wie schon oben geschehen:
| pKS | KS | |
|---|---|---|
| 1. Stufe | 2,16 | 10-2,16mol/L ≈ 0,0069 mol/L |
| 2. Stufe | 7,21 | 10-7,21mol/L ≈ 0,000000062 mol/L |
| 3. Stufe | 12,32 | 10-12,32mol/L ≈ 0,00000000000048 mol/L |
Im Term für Ks stehen jeweils die Konzentrationen der Produkte des Gleichgewichts und damit auch die relevanten Hydroniumionenkonzentrationen im Zähler. Der Wert für Ks der ersten Stufe ist etwa 10.000-mal so groß, wie der der zweiten Stufe. Die zweite Stufe bildet also im Vergleich zur ersten vernachlässigbar wenig Produktmoleküle und trägt dadurch praktisch nicht mehr zur Änderung des pH-Wertes bei. Für die dritte Stufe gilt das in noch viel größerem Maße. Der pH-Wert einer Lösung von Phosphorsäure lässt sich in den meisten Fällen demnach hinreichend genau aus der ersten Protolysestufe berechnen. Die beiden anderen Stufen lassen sich i.d.R. vernachlässigen.
